Ce célèbre casse-tête triangulaire va mettre votre sens de l’observation à l’épreuve
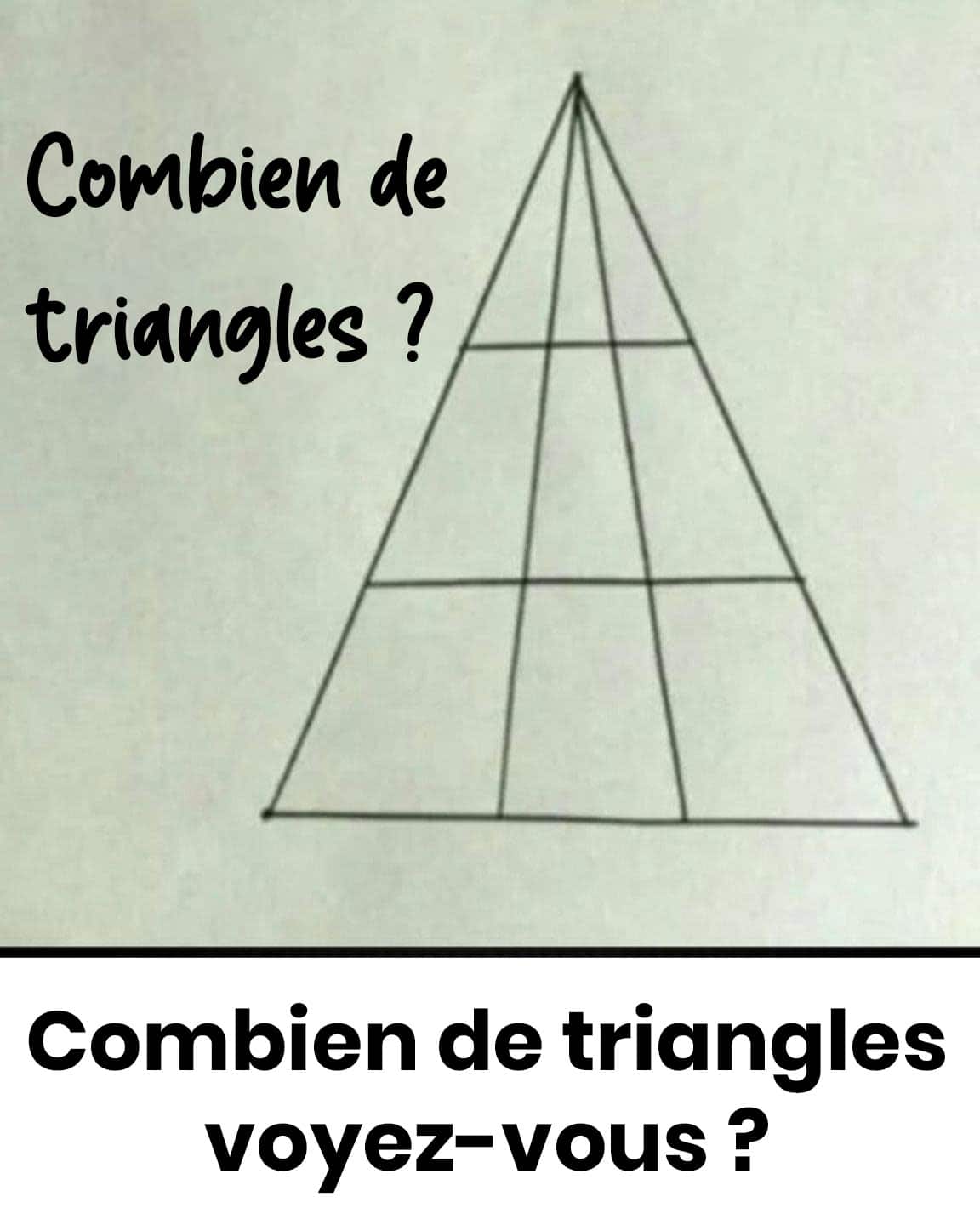
Vous êtes certain·e d'avoir trouvé le bon nombre ? Ce puzzle géométrique réserve bien des surprises. Derrière son apparente simplicité se cachent de multiples figures que notre cerveau a tendance à ignorer. Découvrez la méthode infaillible pour ne plus jamais vous tromper.
L’illusion des triangles invisibles
Notre esprit a naturellement tendance à identifier les triangles les plus apparents tout en négligeant les compositions plus étendues qui regroupent plusieurs sections. Conséquence : on passe systématiquement à côté de certaines formes. Dans cette structure classique (4 niveaux créés par 3 traits parallèles à la base), la solution exacte s’élève à 27.
Si vous avez obtenu 26, vous avez sans doute manqué l’un des grands triangles composites – généralement une figure orientée vers le haut couvrant 3 étages, ou une forme intermédiaire sur l’un des côtés.
La technique progressive pour un décompte précis

Identifiez les triangles « pointant vers le haut » en fonction de leur dimension :
- Dimension 1 niveau : 10
- Dimension 2 niveaux : 6
- Dimension 3 niveaux : 3
- Dimension 4 niveaux : 1
Sous-total des triangles « vers le haut » : 10 + 6 + 3 + 1 = 20.
Incorporez ensuite les triangles « orientés vers le bas » générés par l’assemblage des segments : 7.
Résultat final : 20 + 7 = 27.
Petite astuce mémorielle : retenez « 20 figures ascendantes + 7 figures descendantes » pour contourner l’erreur habituelle.
L’explication claire de la formule mathématique

Vous souhaitez une alternative plus rapide ? Pour une figure triangulaire principale divisée en n rangées grâce à des lignes parallèles à sa base (ici n = 4), cette équation fonctionne parfaitement :
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Avec n = 4 :
T = 4 × 6 × 9 ÷ 8 = 27
Ce chiffre concorde entièrement avec notre estimation méthodique. L’avantage de cette équation, c’est qu’elle intègre automatiquement toutes les configurations imaginables, y compris les assemblages multi-niveaux. Parfait pour confirmer son raisonnement… ou pour remporter une discussion passionnée !
Les pièges courants (et comment s’en préserver)
- Calculer « par étages » sans considérer les grandes figures traversant plusieurs niveaux : l’oubli typique concerne un triangle de 3 niveaux.
- Négliger les triangles inversés (« vers le bas ») : moins évidents visuellement, ils comptent pourtant pour 7 unités.
- Imaginer des lignes verticales supplémentaires : certaines versions incluent effectivement des verticales, ce qui change le résultat (mais jamais pour obtenir 26). Vérifiez toujours la configuration initiale.
- Compter deux fois certaines formes : adoptez une progression méthodique par taille pour éliminer les répétitions.
Pour approfondir le sujet
- Modifiez le nombre de niveaux : expérimentez la formule avec n = 3 ou n = 5 et confrontez avec un calcul manuel – excellent pour aiguiser votre perception.
- Jouez contre la montre : accordez-vous 60 secondes pour parvenir à 27. La clé ? Débutez par les « ascendants », puis ajoutez les « descendants ».
- Transmettez cette connaissance : partager une méthode, c’est l’ancrer durablement dans sa mémoire (et s’assurer de gagner le prochain duel intellectuel).
Car derrière une forme triangulaire élémentaire se dissimule souvent une leçon de logique appliquée… et la satisfaction subtile de conclure en beauté !